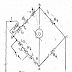
Hay's Bridge

  Hay's Bridge

It is the modification of maxwell's bridge. This bridge uses resistance in series with the standard capacitor.

(unlike the Maxwell's Bridge which uses resistance in parallel with the capacitor).

Let L1 = unknown inductance having resistance R1,

R2, R3, R4= known non-inductive resistances, and C4=standard capacitor.

At balance,

  (R1+jwL1)(R4-j/wC4)=R2.R3

Separating real and imaginary terms and solving we get :

                L1=(R2.R3.C4)/(1+w^2.C^2.R4^2)

and          R1= (w^2.R2.R3.R4.C4^2)/(1+w^2.C4^2.R4^2)

The Q factor of the coil is : Q= (wL1)/R1 = 1/(wC4R4)

there is a frequency term in the above expressions so it seems that it must be accurately known. This is not true for inductance when a high Q coil is being measured. Because:

we can write 

L1= (R2.R3.C4)/(1+(1/Q)^2)

for Q value higher than 10  the equation reduces to L1= R2.R3.C4

we can see the eq. becomes the same as maxwell's bridge.

Advantages:

• This bridge gives a very simple expression for unknown inductance for high Q coils and is suitable for coils having Q>10.
• This Bridge gives a simple expression for the Q factor.
• If we examine the expression for Q factor: Q = 1/(w.C4.R4)

R4 appears in denominator means for a high value of Q we have a small value of R4 thus bridge requires a low value of R4 whereas The Maxwell's bridge requires a parallel resistor, R4 of a very high value.

Disadvantages:

• The bridge is not suitable for the measurement of inductance Q <10.

Reference:

Swerny