Anderson's Bridge

 Introduction

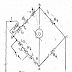
This Bridge, in fact, is a modification of maxwell's inductance capacitance bridge in this method we measure unknown self-inductance in terms of a standard capacitor this method is applicable for the precise measurement of self-inductance over a wide range of values.

Let L1=Self inductance be measured,

      r1= resistance connected in series with-inductor,

r, R2, R3, R4= known non-inductive resistances,

R1= resistance of the self inductor,

C= fixed standard capacitor.

At balance , I1=I3 and I2 = Ic + I4

Writing and solving balance equations gives us the result 

and

Two obtain easy convergence of balance alternate adjustments of r1 and r are done.

Advantages:

• for a low-value Q coil it is easy to obtain a balance point because there is no sliding occurs like maxwell's bridge.
•  A fixed capacitor is used instead of a variable capacitor like in maxwell's bridge.
• This bridge may be used for accurate measurement of capacitance in terms of inductance

Disadvantages:

• The bridge is more complex than maxwell's bridge, due to more parts it is difficult to manipulate the bridge for different measurements and also to set up . The balance equations are not simple and in fact tedious.

Considering the above complications in the cases where a variable capacitor is permissible maxwell's bridge is used.